Η μέρα του π (μια συνεργασία του Γιάννη Μαλλιαρού)

Σήμερα είναι 14 Μαρτίου, δηλαδή 14/3, δηλαδή 3/14 με την αμερικάνικη σημειογραφία -ταιριάζει λοιπόν να δημοσιεύσουμε μια συνεργασία του φίλου μας του Γιάννη Μαλλιαρού για τον αριθμό π. Αυτό σημαίνει πως τα χρονογραφήματα του παππού μου παίρνουν μετάθεση για αύριο. Χωρίς άλλα δικά μου, ο λόγος στον Γιάννη.

14 Μαρτίου σήμερα κι όπως έχει αναφερθεί πριν 7 χρόνια, σήμερα είναι η μέρα του π: «14/3 δηλαδή, κι άμα το γράψουμε αμερικανοπρεπώς είναι 3/14, οπότε δεν είναι ανεξήγητο που διάλεξα αυτή την ημερομηνία για να παρουσιάσω ένα άρθρο αφιερωμένο στο π» έγραφε τότε ο Νικοκύρης και συνέχιζε κάνοντας μια μικρή αναφορά στον αριθμό π που έδωσε την ευκαιρία για το άρθρο εκείνο και συνέχιζε για το γράμμα π. Κάποια στιγμή το Σεπτέμβρη σε άρθρο για τους μνημονικούς κανόνες των μαθητών αναφέρθηκαν τα ποιηματάκια που δίνουν κάποια ψηφία του π και πηγαίνοντας στο παλιό εκείνο άρθρο είδα πως τα είχα γράψει στο 200στό από τα 202 σχόλια και μάλιστα δυο μέρες μετά από τη δημοσίευση του άρθρου (που ήταν και καθαροδευτέρα κι εγώ βόλταρα στη Ρόδο), άρα λίγοι τα είδαν. Τότε πρότεινα να γραφτεί ένα άρθρο για τον αριθμό π και μάλιστα είπα πως μπορώ να το γράψω εγώ μιας και είχα ασχοληθεί λίγο με εργασίες στο σχολείο για το π.

Το π τον αριθμό είπα. Αλλά γιατί το π είναι αριθμός; Γιατί με π συμβολίζεται διεθνώς ο λόγος (το πηλίκο) του κύκλου προς τη διάμετρό του (και αν δεν έχουν στο αλφάβητό τους το π και θέλουν να το τυπώσουν το βάζουν όπως ακούγεται π.χ. pi). π από το περιφέρεια, το γύρω του κύκλου (που σήμερα το λέμε κύκλο σκέτα και τελειώνουμε). Που όποιον κύκλο και να πάρουμε ο λόγος αυτός είναι σταθερός, περίπου 3,14. Αλλά επειδή μας διαβάζουν και άνθρωποι που δεν είναι των θετικών επιστημών ας πω τι είναι κύκλος και τι διάμετρος.

Κύκλος είναι το στρογγυλό σχήμα, αυτό που στο σχολείο το φτιάχναμε με το διαβήτη. Εκεί που βάζουμε τη μύτη του διαβήτη είναι το κέντρο του και η γραμμή που γράφει το μολύβι (ή το στιλό ή η κιμωλία ή ό,τι υπάρχει στην άλλη άκρη του) είναι ο κύκλος. Το άνοιγμα του διαβήτη είναι η ακτίνα που συνήθως συμβολίζεται με r. Και διάμετρος είναι ένα ευθύγραμμο τμήμα που τα άκρα του βρίσκονται πάνω στον κύκλο (δηλ. μια χορδή) αλλά περνάει κι από το κέντρο του κύκλου. Συνήθως τη διάμετρο τη συμβολίζουμε με δ, είναι ίση με δυο ακτίνες του κύκλου (2r) κι έτσι στο σχολείο μαθαίναμε (κι έτσι είναι δηλαδή) πως ο κύκλος είναι ίσος με π επί δ ή με 2πr.

Το π χώνεται και σ’ άλλους τύπους που έχουν να κάνουν με κυκλικά σχήματα, αλλά δεν χρειάζεται να μπλέκουμε. Στην εικόνα της αρχής η διαδικασία νομίζω φαίνεται καθαρά: παίρνουμε μερικές διαμέτρους ενός κύκλου τη μια δίπλα απ’ την άλλη, σημειώνουμε ένα σημείο για αρχή κι αρχίζουμε να κυλάμε τον κύκλο οπότε βλέπουμε πως το ίδιο σημείο ξαναπατάει κάπου μετά το 3 (ή βάζουμε μια κορδέλα γύρω απ’ τον κύκλο, την ξετυλίγουμε και βλέπουμε το ίδιο πράγμα).

Ιστορία προσδιορισμού του π

Όπως είπα, πολύ νωρίς οι άνθρωποι  προσπαθούσαν να υπολογίσουν τον λόγο αυτό αφού κατάλαβαν πως είναι σταθερός (άσχετα πως τον έλεγαν και τον περιέγραφαν – ο συμβολισμός με το π είναι τα τελευταία 300 χρόνια περίπου – και προσοχή μόνο μικρό και γραμμένο έτσι, σαν πορτούλα, όχι το καλλιγραφικό που δείχνει κάτι άλλο ούτε το κεφαλαίο Π που σημαίνει γινόμενο). Βαβυλώνιοι, Εβραίοι, Αιγύπτιοι, Έλληνες, Άραβες, Ινδοί, Κινέζοι, Ευρωπαίοι, Ιάπωνες, Αμερικανοί ασχολήθηκαν μαζί του.

Ας πούμε ήδη οι Βαβυλώνιοι το υπολόγιζαν περίπου 3 αλλά αν ήθελαν παραπάνω ακρίβεια ήξεραν κι έβαζαν δηλ. 3,125. Οι Αιγύπτιοι, το 1800 π.Χ. το υπολόγιζαν 3,16… (έδιναν για το εμβαδόν του κύκλου τον τύπο ). Ο π αναφέρεται και στην Παλαιά Διαθήκη (Βασιλειών Ζ) «καὶ ἐποίησε τὴν θάλασσαν δέκα ἐν πήχει ἀπὸ τοῦ χείλους αὐτῆς ἕως τοῦ χείλους αὐτῆς, στρογγύλον κύκλῳ τὸ αὐτό· πέντε ἐν πήχει τὸ ὕψος αὐτῆς, καὶ συνηγμένοι τρεῖς καὶ τριάκοντα ἐν πήχει ἐκύκλουν αὐτήν«. Δηλαδή με διάμετρο 11 ο κύκλος είχε μήκος 33, άρα για τους Εβραίους π=3.

Οι (αρχαίοι) Έλληνες προσπαθούν να υπολογίσουν το π με διάφορους τρόπους. Κύριος στόχος ο τετραγωνισμός του κύκλου: Να φτιαχτεί (με κανόνα και διαβήτη) ένα τετράγωνο που να έχει ακριβώς το ίδιο εμβαδόν μ’ έναν κύκλο. Είχαν βρει πως κάθε πολύγωνο μπορεί να γίνει τετράγωνο με ίσο εμβαδόν Γιατί όχι και ένα καμπυλόγραμμο σχήμα; Ο Ιπποκράτης ο Χίος (5ος αιώνας π.Χ) καταφέρνει να τετραγωνίσει καμπυλόγραμμο σχήμα. Είναι οι μηνίσκοι του Ιπποκράτη που το εμβαδόν δυο μηνίσκων (ό,τι μένει όταν κόβονται δυο κύκλοι) είναι ίσο με το εμβαδόν ορθογωνίου τριγώνου άρα φτιάχνεται και τετράγωνο. Υπέροχα, αλλά…

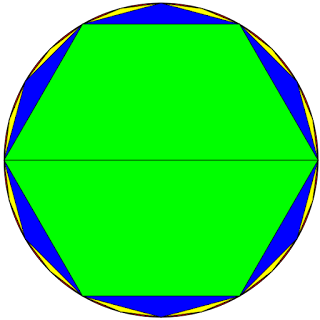
Έγινε προσπάθεια να προσεγγιστεί ο κύκλος με διαδοχικά πολύγωνα όπως στο σχήμα. Γράφουμε ένα πολύγωνο, μετά ένα επόμενο με διπλάσιες κορυφές, ξανά το ίδιο και πάει λέγοντας. Όπως βλέπουμε όσο πιο πολλές κορυφές τόσο πιο κοντά στον κύκλο. Όμως πάντα κάτι μένει (για παράδειγμα στο παραπάνω σχήμα υπάρχει λίγο κοκκινάκι. Δεν το βλέπει το μάτι, αλλά αν μεγαλώσει το σχήμα κατάλληλα, θα φανεί. Τα χρόνια περνάνε και φτάνουμε στον Αρχιμήδη.

Αυτός δίνει τον τύπο του εμβαδού (πr2 – εντάξει, όχι έτσι, περιγραφικά, ημιπεριφέρεια επί ακτίνα) και προσδιορίζει ότι πάει να πει πως το π είναι ανάμεσα στο 3,14084 και το 3,14285. Πολύ καλή ακρίβεια αν σκεφτούμε πως σήμερα ξέρουμε πως π=3,14159 (και η έκφραση ήταν με κλάσματα, μόνο ρητοί αριθμοί γίνονταν δεκτοί). Πώς το κατάφερε; Παίρνοντας πολύγωνα όχι μόνο μέσα αλλά και έξω απ’ τον κύκλο (όχι μόνο εγγεγραμμένα αλλά και περιγεγραμμένα).

Όμως ο π είναι αριθμός άρρητος και υπερβατικός: (πάλι μαθηματικά) Άρρητοι αριθμοί είναι αυτοί που δεν μπορούν να γραφούν σε μορφή κλάσματος (γιατί τα κλάσματα μπορούμε να τα πούμε, είναι ρητοί). Κι αυτοί είναι αριθμοί που έχουν άπειρα δεκαδικά ψηφία που δεν έχουν κάποια σταθερή σειρά. Το δεύτερο λέει πως δεν μπορούμε να τον πάρουμε σαν ρίζα κάποιας εξίσωσης με συντελεστές ακέραιους αριθμούς. Ζόρικη περίπτωση.

Οι Ρωμαίοι τον υπολόγιζαν με 3,125 (πάλι πίσω). Οι Κινέζοι τον 1ο μ.Χ. αιώνα τον υπολογίζουν στο 3,1547. Τον 3ο πήγε στο δηλαδή 3,15555. Αργότερα πάνε στο δηλαδή στο 3,1416 και τον 5ο αιώνα τον υπολογίζουν στο 3,14159265 και ναι, είναι όλα αυτά σωστά τα ψηφία. Την ίδια εποχή περίπου οι Ινδοί τον υπολογίζουν στο 3,1416. Αργότερα τον κάνουν ρίζα του 10 (3,1627) ενώ τον δωδέκατο αιώνα πάμε στα (δηλαδή 3,14285 το άνω όριο του Αρχιμήδη). Στα ίδια είναι και οι Άραβες τον 9ο αιώνα, στα ίδια και οι Πέρσες Αν και στη Σαμαρακάνδη είχαν ήδη συμπέσει με τους Κινέζους στο 3,14159265. Με εγγεγραμμένα πολύγωνα το πέτυχαν αλλά κατάφεραν να υπολογίσουν αρκετές πλευρές: 230!

Επιστρέφουμε προς τη δύση. 13ος αιώνας κι ο Φιμπονάτσι (Fibonacci) δίνει π=3,141818. Καμιά διακοσαριά χρόνια αργότερα π=3,1459265358979 και σε άλλα τόσα π=3,1415926536 (τα πρώτα δεκαδικά φαίνεται να σταθεροποιούνται). Νεύτωνας π=3,1415926535897932

Ο Όιλερ (Euler) σκέφτεται πως είναι υπερβατικός αριθμός (τότε εμφανίζεται αυτή η κατηγορία) κάτι που αποδεικνύεται το 1883 ενώ το 1761 ο Λάμπερτ (Johann Heinrich Lambert) αποδεικνύει ότι  ο π είναι άρρητος. Έτσι το θέμα πια δεν είναι ο τετραγωνισμός του κύκλου αλλά το πόσα ψηφία του π μπορούν να υπολογιστούν. Τον 20ό αιώνα στο παιχνίδι μπαίνουν οι υπολογιστές και τα ρεκόρ των ψηφίων του π που έχουν υπολογιστεί καταρρίπτονται το ένα μετά το άλλο (τελευταία έχουν φτάσει τα τρισεκατομμύρια δεκαδικά).

Σχετικά με τα ψηφία του π

Σε σταθμό του μετρό της Βιέννης. Ο διάδρομοι πρόσβασης έχουν διάφορα νούμερα (πόση ενέργεια ξοδεύεται κάθε στιγμή, πόσος είναι ο πληθυσμός της γης, πόσοι πεθαίνουν κλπ). Δεν μπορούσε να λείπει το π. Με ορισμό στην αρχή

Άρρητος ο π (συνήθως λέω – γράφω ο π, εννοώντας ο αριθμός π, αν και μπορεί να χρησιμοποιήσω και το π κάποιες φορές) άρα με άπειρα (δεκαδικά) ψηφία που εμφανίζονται με τυχαία σειρά αλλά η αναλογία του κάθε ψηφίου (0 … 9) είναι ίδια, δεν υπάρχει κάποιο προτιμώμενο ψηφίο. Έτσι όπως εμφανίζονται μπορούμε να βρούμε ανάμεσά του όποια αριθμοσειρά θέλουμε. Την ημερομηνία γέννησης (είτε 02/03/1932 είτε 2/3/22 είτε μ’ όποια μορφή διαλέξουμε – εννοείται χωρίς κάθετες) ή τον αριθμό τηλεφώνου του σταθερού ή του κινητού μας. Βέβαια, σε ποια θέση θα ξεκινάει είναι ένα θέμα. Τη δικιά μου ημερομηνία γέννησης δεν κατάφερα να την εντοπίσω στο πρώτο εκατομμύριο ψηφία του ενώ η ακολουθία 123456789 εμφανίζεται για πρώτη φορά στο 523.551.502ο ψηφίο.

και μπόλικα δεκαδικά στη συνέχεια.

Και πόσα είναι τα απαραίτητα ψηφία του π για τους υπολογισμούς μας; Η απάντηση εξαρτάται από το τι θέλεις να υπολογίσεις. Οι μηχανικοί συνήθως το υπολογίζουν 3. Χωρίς κανένα δεκαδικό. Αν πιάσουν το κομπιουτεράκι τους που έχει αποθηκευμένον τον π τότε πατάνε το σχετικό πλήκτρο και τους χώνει δεκαδικά (όσα έχει στη μνήμη). Στα μαθηματικά και στη φυσική έχουμε το 3,14 κι είμαστ’ εντάξει (αν και λέμε στα παιδιά πως υπάρχουν παραπάνω δεκαδικά και όσα απ’ αυτά που ανέφερα παραπάνω αποφασίσουμε).

Ναι, αλλά όταν θέλουμε μεγάλη ακρίβεια; Π.χ. η ΝΑΣΑ στις αποστολές της πόσα χρησιμοποιεί; Η απάντηση είναι μόλις 15. Δηλαδή 3,141592653589793. Είναι αρκετά; Ναι. Αν βάλουμε τη διάμετρο της Γης και θέλουμε να υπολογίσουμε τον αντίστοιχο κύκλο (δεν λέω ποιον, ανάλογα σε ποιο σημείο θα πάρουμε διάμετρο 😀) η διαφορά απ’ την πραγματική τιμή είναι μικρότερη από ένα μικρό μόριο. Ή αν πάρουμε την απόσταση που έχει διασχίσει ένα από τα Βόγιατζερ (διαστημόπλοια που εκτοξεύτηκαν πριν 50 περίπου χρόνια κι από τότε όλο και απομακρύνονται απ’ τη Γη έχοντας φτάσει – ή περάσει –  στα άκρα του ηλιακού συστήματος) και υπολογίσουμε τον κύκλο που έχει για ακτίνα αυτή την απόσταση. Ε, η διαφορά ανάμεσα στην τιμή με τα 15 δεκαδικά και την πραγματική θα ήταν 4 – 5 εκατοστά!

Τότε γιατί γίνεται τόση φασαρία για να υπολογίσουμε όλο και περισσότερα ψηφία του π; Μα γιατί μπορούμε. Δεν υπάρχει άλλος λόγος.

Ποιήματα για το π

Για να θυμούνται οι άνθρωποι τα ψηφία του π έφτιαξαν μνημονικούς κανόνες (από κει που ξεκινήσαμε το άρθρο). Κι οι μνημονικοί κανόνες είναι πιο ευκολομνημόνευτοι αν είναι σαν ποιήματα. Ένα πολύ γνωστό σε μας τους Έλληνες είναι το «αεί ο θεός ο μέγας γεωμετρεί». Μετρώντας τα γράμματα κάθε λέξεις έχεις το ψηφίο της συγκεκριμένης θέσης. Αεί 3, ο 1, θεός 4, ο 1, μέγας 5, γεωμετρεί 9 και πάει λέγοντας. Το ιδιαίτερο που έχει αυτός ο κανόνας είναι πως δίνει με αριστοτεχνικό τρόπο τον ορισμό του π. Αυτές οι πρώτες λέξεις αποδίδονται στον Πλάτωνα (αλλά όχι για να περιγράψει το π) και η συνέχεια είναι του Νικ. Χατζηδάκη, καθηγητή μαθηματικών του Πανεπιστημίου Αθηνών. Ιδού το ολόκληρο:
«Αεί ο Θεός ο μέγας γεωμετρεί, το κύκλου μήκος ίνα ορίση διαμέτρω, παρήγαγεν αριθμόν απέραντον, και ον φευ, ουδέποτε όλον θνητοί θα εύρωσι» 3,1415926535897932384626. Μπόλικο πράμα. 23 δεκαδικά. Βέβαια σε καθαρεύουσα και με επιλογή της διάταξης αλλά είναι ωραίο (κατά τη γνώμη μου).

Με παρόμοιο τρόπο, με τον αριθμό γραμμάτων έχουμε και σε άλλες γλώσσες. Πολλές κάνουν τιμητική αναφορά στον Αρχιμήδη. Κάποιες έχουν σε ποίημα τα νούμερα. Ενώ άλλες είναι κάτι τελείως άσχετο. Ιδού μερικά (με τις μεταφράσεις τους – ελάχιστες από μένα οι άλλες όπως τις βρήκα).

Αγγλικά

Three point one four one five nine two
Its been around forever – its not new
It appears everywhere in here and in there
its irrational I know but its true
(Τρία κόμμα ένα τέσσερα ένα πέντε εννιά δύο
Κυκλοφορεί πάντα – δεν είναι καινούργιο
Εμφανίζεται παντού εδώ και εκεί μέσα
είναι παράλογο το ξέρω αλλά είναι αλήθεια)

How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics. All of the geometry, Herr Planck, is fairly hard
3,14159265358979323846264
(Πόσο θέλω ένα ποτό, αλκοολούχο φυσικά, μετά τις βαριές διαλέξεις που αφορούν την κβαντομηχανική. Όλη η γεωμετρία, κύριε Πλανκ, είναι αρκετά δύσκολη)

[επίτηδες ανορθόγραφα γραμμένο το όνομα του Αρχιμήδη για να βγει το νούμερο 9]
How I wish I could recollect, of circle round, the exact relation Arkimedes learned
3,1415926535897
(Πόσο θα ‘θελα να θυμάμαι από τον στρογγυλό κύκλο την ακριβή σχέση που γνωρίζει ο Αρχιμήδης)

Γερμανικά
Wie, o dies π macht ernstlich so vielen viele Müh
3,141592653
(Πώς, ω αυτό το πι όντως δημιουργεί σε τόσο πολλούς τόσο μεγάλο πρόβλημα.)

Ιταλικά
Che n’ ebbe d’ utile Archimede da ustori vetri sua somma scoperta?
3,14159265358
(Τι καλό βρήκε ο Αρχιμήδης από τη μεγάλη του ανακάλυψη τα κάτοπτρα που πυρπολούν;)

Πορτογαλέζικα
Sim, é útil e fácil memorizar um número grato aos sábios.
3,1415926535
(Ναι, είναι χρήσιμο να απομνημονεύσεις έναν αριθμό χρήσιμο στους σοφούς)

Ρουμάνικα
Aşa e bine a scrie renumitul şi utilul număr.
3,14159265
(Αυτός είναι ο τρόπος να γράψεις το φημισμένο και χρήσιμο αριθμό)

Ρώσικα
Это я знаю и помню прекрасно
3,14159
(Αυτό το ξέρω και το θυμάμαι τέλεια)

Γαλλικά
Que j’aime à faire apprendre un nombre utile aux sages !
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut priser la valeur?
3,141592653587932384626

ή σε μεγαλύτερη έκταση

Que j’aime à faire apprendre un nombre utile aux sages!
Immortel Archimède, artiste ingénieur,
Qui de ton jugement peut priser la valeur?
Pour moi, ton problème eut de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l’admirable procédé, l’œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l’espace plan circulaire?
Former un triangle auquel il équivaudra?
Nouvelle invention: Archimède inscrira
Dedans un hexagone; appréciera son aire
Fonction du rayon. Pas trop ne s’y tiendra:
Dédoublera chaque élément antérieur;
Toujours de l’orbe calculée approchera;
Définira limite; enfin, l’arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle

(Πόσο μου αρέσει να διδάσκω αυτόν τον χρήσιμο στους σοφούς αριθμό!
Αρχιμήδη αθάνατε, καλλιτέχνη μηχανικέ,
Ποιος του νου σου μπορεί να εκτιμήσει την αξία;
Για μένα, το πρόβλημα σου είχε τόσα προτερήματα.
Παλιά, μυστήριο, ένα πρόβλημα εμπόδιζε
Όλη τη θαυμάσια εξέλιξη, το μεγαλειώδες έργο
Που ο Πυθαγόρας αποκάλυψε στους αρχαίους Έλληνες.
Ω τετραγωνισμέ! Παλιό μαρτύριο του φιλοσόφου!
Άλυτη σφαιρικότητα, για πολλά χρόνια προκαλέσατε
τον Πυθαγόρα και τους μιμητές του.
Πώς να κατανοήσει κανείς το κυκλικό επίπεδο διάστημα;
Να σχηματίσει ένα τρίγωνο με το οποίο θα ισούται;
Καινούργια ανακάλυψη: ο Αρχιμήδης θα εγγράψει
Μέσα ένα εξάγωνο θα υπολογίσει το εμβαδόν του
Συναρτήσει της ακτίνας. Δεν θα παραμείνει για πολύ:
Θα διπλασιάσει κάθε προηγούμενο στοιχείο
Πάντα προσεγγίζει την υπολογισμένη κυκλική τροχιά
Θα ορίσει όριο δηλαδή, το τόξο, τον οριοθέτη
Αυτού του αλλόκοτου κύκλου, εχθρού πάρα πολύ ανυπότακτου!
Καθηγητή, δίδαξε το πρόβλημα του με ζήλο!)

Αρκετά από τα παραπάνω στοιχεία είναι στο http://www.math.uoa.gr/me/dipl/dipl_aroni.pdf